广义递归论

把在自然数集上定义的递归论(古典递归论)推广到其它数学结构上去而得到的数学理论。常见的有序数上的递归论和高类型对象的递归论。

将自然数推广为序数，讨论序数上的递归函数，是广义递归论的一个方面。这种推广有两种选择：一是把论域推广到整个序数类ON上，一是把论域推广到序数类的某个前节α上，两种选择的方法和概念相似，比较受人重视的是后一种选择，称为α递归论。

建立α递归论可以像建立古典的部分递归函数那样，先讨论原始递归函数，再增加μ算子；也可以在序数α上定义图灵机，等等。目前使用较多的是克里普克等人参照一般递归函数所建立的等式系统的方法。克里普克的等式系统是在艾尔布朗－哥德尔－克利尼的等式系统(参见一般递归函数)上增加一条无穷规则，以保证计算能进行到α步。由有穷的等式集出发，利用这些规则所能演绎出的函数就叫α递归函数；α递归函数的值域称为α递归可枚举集。

并不是每个序数都可以作为α递归函数的论域，例如ω+2就不行——它对加法不封闭。

如果对任给的有穷等式集，其全部后承都可在α步之内演绎出来，则称α为可允许序数。以可允许序数作为论域，就可以保证所定义的函数对α封闭，而且所定义的α递归函数也都能在α步之内计算。α递归论就是以任何可允许序数为论域的递归函数论。

古典递归论的许多结果都与“有穷”有关，在α递归论中，与“有穷”相应的概念是α有穷：小于α的序数β称为α有穷数，如果Sα，且存在α有穷数β和α递归函数f使S是β在f下象集(即S=f［β］)，则称S为α有穷集。按这个定义，α有穷并不仅指基数小于α，这一点与古典递归论的情况有所不同。这种区别导致α递归论的某些结果与古典递归论有所不同。

古典递归论中的概念、方法都可推广到α递归论中，例如多一归约，m度，图灵归约，图灵度，等等。对α递归函数的图灵度空间的研究也是α递归论的重要课题，也有有穷损害(0′)优先方法、无穷损害(0″)优先方法等等。

还可以把古典递归论推广到高类型对象上去。

对每个自然数j，定义类型为j的对象集T：

T=N(自然数集)

T=从T到N的全体全函数的集合，所谓高类型对象是指集合

中的元素。

有穷序列x=(x，…，x)∈T称为高类型点。如果x，…，x分别是类型为j，…，j的对象，则称max(j，…，j)为点x的类型。以T表示全体高类型点的集合。

在T上可以定义连接运算t(x，y)：

若x=(x，…，x)，y=(y，…，y)，则t(x，y)=(x，…，x，y，…，y)

设是A=T上的一个合适的泛函类(参见递归泛函)，如果它还含有以下三个函数(i)～(iii)，并对规则(iv)、(v)封闭，则称之为克利尼类(以下以x、y、z表示T中的点，σ，τ表示T中的有穷点列(可以为空))：

(i)类型指示函数：

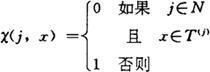
(ii)长度函数

len(x)=n，如果x=(x，…，x)

(iii)类型为1的对象的使用(函数)

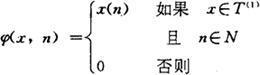
(iv)类型大于1的对象的使用：从F(x，y，σ，f一)，对j∈N，可得Gj：

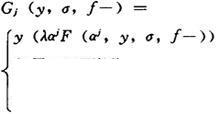
(其中，α表示T中的变元)。

(v)．对连接函数、投影函数的代入。

设是一克利尼类，φ是定义在T的某个子α集上，以自然数为值的函数(T上的部分函数)，其定义域是=X×X…×XT，则φ本身也是一个泛函。如果φ作为泛函是递归的，即称φ是递归函数。换句话说，就是存在的泛函F(σ，x，f)和自然数n，…，n使

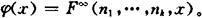
高类型递归论就是把古典递归论的概念、方法推广到递归函数(参见递归泛函)