模态代数语义
模态逻辑的代数语义。模态代数语义是模态逻辑发展史上较早出现的语义解释,奠基人是J.C.C.麦金西(Mckinsey,1908~1953)和A.塔尔斯基(Tarski,1902~1983)。在克里普克关系语义于20世纪50年代末提出以后,模态代数语义几乎在文献中消失了,直到70年代才得到复兴。模态代数语义的基本概念是模态代数。一个模态代数 =〈A,0,1,-,∩,∪,l,m〉由一个布尔代数〈A,0,1,-,∩,∪〉和A上的两个满足下列条件的一元运算1,m组成:
=〈A,0,1,-,∩,∪,l,m〉由一个布尔代数〈A,0,1,-,∩,∪〉和A上的两个满足下列条件的一元运算1,m组成:

A上的一个赋值v就是从命题到 中元素的一个映射,满足下列条件:
中元素的一个映射,满足下列条件:

一个代数模型( ,v)由一个模态代数
,v)由一个模态代数 和这代数上的一个赋值v组成。称一个命题A在代数模型(
和这代数上的一个赋值v组成。称一个命题A在代数模型( ,v)中为真,当且仅当,v(A)=1。称A在模态代数
,v)中为真,当且仅当,v(A)=1。称A在模态代数 上有效(记成
上有效(记成
 A),当且仅当,它在
A),当且仅当,它在 上的任一个模型中都为真。极小正规模态系统K的定理在任一个模态代数上都有效。对K附加不同的公理产生新的模态系统相当于对模态代数附加不同的要求,例如熟知的正规模态系统S4由K附加公理□P
上的任一个模型中都为真。极小正规模态系统K的定理在任一个模态代数上都有效。对K附加不同的公理产生新的模态系统相当于对模态代数附加不同的要求,例如熟知的正规模态系统S4由K附加公理□P P和□P
P和□P □□P而得,使S4中所有定理都有效的模态代数
□□P而得,使S4中所有定理都有效的模态代数 =〈A,0,1,-,∩,∪,l,m〉必须满足l(a)≤a和l(l(a))=l(a)的要求,即,
=〈A,0,1,-,∩,∪,l,m〉必须满足l(a)≤a和l(l(a))=l(a)的要求,即, 必须是麦金西和塔尔斯基的闭包代数。
必须是麦金西和塔尔斯基的闭包代数。
一个克里普克标架(W,R)决定一个模态代数〈 (W),
(W), ,W,-,∩,∪,l,m〉,这里
,W,-,∩,∪,l,m〉,这里 (W)是W的幂集,
(W)是W的幂集, 是空集,-、∩、∪是通常集合的补、并、交运算,l和m的定义如下:
是空集,-、∩、∪是通常集合的补、并、交运算,l和m的定义如下:
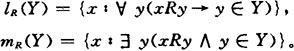
由(W,R)决定的模态代数和(W,R)是等价的,也就是说,一命题在(W,R)上有效当且仅当它在(W,R)所决定的模态代数上有效。类似地,一个标架 =(W,R,P)也决定一个与之等价的模态代数
=(W,R,P)也决定一个与之等价的模态代数 =〈P,
=〈P, ,W,-,∩,∪,l,m〉,这里
,W,-,∩,∪,l,m〉,这里 、-、∩、∪、l、m的意义都同上所述。反之,一个模态代数
、-、∩、∪、l、m的意义都同上所述。反之,一个模态代数 =〈A,0,1,-,∩,∪,l,m〉也决定一个标架
=〈A,0,1,-,∩,∪,l,m〉也决定一个标架 =(
=( ,
, ,
, ),这里
),这里 由
由 的所有超滤组成,
的所有超滤组成, 和
和 的定义如下:
的定义如下:

所谓 的超滤是指A的满足下列条件的子集F:
的超滤是指A的满足下列条件的子集F:
(1)1∈F但0 F;
F;
(2)若a,b∈F则a∩b∈F;
(3)若a∈F且a≤b(即,a∩b=b)则b∈F;
(4)对各个a∈A,不是a∈F就是 ∈F。
∈F。 和
和 是等价的。因此,模态代数语义等价于一般关系语义,克里普克关系语义和正规邻域语义都真包含于模态代数语义。模态代数语义在70年代得到了很大发展,建立起了模态逻辑的对偶理论。
是等价的。因此,模态代数语义等价于一般关系语义,克里普克关系语义和正规邻域语义都真包含于模态代数语义。模态代数语义在70年代得到了很大发展,建立起了模态逻辑的对偶理论。