优先方法

递归论中用以构造图灵度的一种强有力的方法。优先方法最早是由弗里德伯格(Friedberg)和穆契尼克(Muchnik)在20世纪50年代创立的，他们各自独立地用这种方法解决了波斯特问题。弗里德伯格和穆契尼克所用的方法后来称为有穷损害的优先方法。60年代，舍恩菲尔德(Shoenfield)和萨克斯(Sacks)等人又创立了无穷损害的优先方法。优先方法的创立使得对图灵度的认识大大向前推进。有关图灵度结构的定理(参见图灵度)大部分都是用优先方法证明的。利用优先方法研度图灵度的结构至今仍是递归论中的主要课题。

构造某个图灵度，实际上就是构造该度的一个代表元素(一个自然数集)A。所要求的性质常用一个无穷的需求序列R，R，R，……来表示。如果n＜m，就称需求R优先于R。

构造的过程是从空集出发，通过一个递归的过程，逐次加入一个或多个(可以是无穷多个)元素，形成递归的集合序列

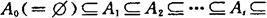
…(A称为第s步构造的集合)，构造的过程要求第s步使R得到满足。

由于各需求未必是彼此独立的，因而在构造过程中，为了满足某个R，可能会使已经得到满足的某个R(s＜t)受到损害(称R在第t步受到损害)，为了使每个需求最终都得到满足是——即A=A满足全部需求——就要求构造的过程有一种自动补偿功能：一个需求R无论被损害多少次，最终总能得到保证。

如果在整个构造过程中每个需求都只受到有穷次损害，则称之为有穷损害的优先方法。如果有的需求受到无穷多次损害，则称之为无穷损害的优先方法。

在使用优先方法构造出某个集合A时，在整个构造过程的末尾常需要一个Φ的神谕以便认定每个需求都得到满足。视其中的n=1，2，3等等可将优先方法分成0′优先方法、0″优先方法、优先方法等等。

用优先方法构造的集合，其本身和其余集都是无穷的(否则就是递归集，用不着如此构造了)。因而需求可以分成两类：一类是要求将某些数放入A，称之为正需求，一类是要求某些数永远不放入A，称为负需求。正需求记作｛P｝，负需求记作｛N｝。

下面以一个有穷损害优先方法(0′优先方法)的例子简单说明一下具体的构造过程。

定理 存在一个单纯集A，使A′≡Φ′。(由此可推出A是递归可枚举集，但A既不是递归集也不是T完全的递归可枚举集。参见图灵归约、跳跃算子和波斯特问题。)

要A是单纯集，需要保证三点、

(1)、A是递归可枚举集；

(2)、是无穷集；

(3)、A不包含无穷的递归可枚举子集。

只要构造序列

的过程是递归的，就可以保证(1)；只要坚持每向A中放入一个数也向中至少放一个数，就可以保证(2)(参看后面具体构造过程的条件(1．2)中第二个合取分量：x＞2i)。

为了满足(3)，需要在每个无穷的递归可枚举集中都选出一个元素放入A中，这就是正需求：

P：如果W无穷，则W∩A≠Φ。

负需求

则保证了

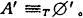
这一点并不是一目了然的，需要做点说明。

负需求中的“(s)…”表示“存在无穷多个s……。记号｛e｝(x)有穷(详见后面的具体构造过程)，所以｛e｝(e)Φ′(参见极限定理)，而(e)就是A′的特征函数。于是A′≤Φ′，因而负需求保证

于是

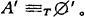
(Φ′≤A′是当然的)。

函数u(A；e，x，s)称为使用函数，其定义为：

u(A；e，x，s)

函数r(e，s)=u(A，e，e，s)称为抑制函数，只要我们构造｛A｝∈的过程是递归的。r(e，s)就是递归函数。

当AA…A构造好之后，如果｛e｝(e)?”中的n都小于r(e，s)。因而只要今后不再向A中放入小于r(e，s)的数，所得到的各个A(s＜t)都仍保持｛e｝(e)，而且可保证｛e｝(e)=｛e｝(e)。

但是，对于某些i＜e，为了使P得到满足，可能还需要向A中加入小于r(e，s)的数。不过对每个e，这样的情形至多只会出现e次，因而N至多被损害e次。

实际的构造过程如下：

第0步，A=Φ，

第s+1步：As构造好以后，对每个e，都可以计算r(e，s)，取满足以下两个条件的最小的i≤s，

(其中W表示W中最先被枚举出来的s个元素)。

如果存在这样的i，就将满足(1．2)的最小x放入A：A=A∪｛x｝；否则令A=A(由于每一步至多增加一个元素，故A都是有穷集)。

放入x之后，(1．1)就不满足了，从而P得到满足，而且此后P不会受到损害。

最后，令A=A。