布尔代数

现代逻辑中经常应用的一种数学结构。布尔代数的基本概念是G．布尔1847年提出的。1904年E．V．亨廷顿给出了布尔代数的公理。

在一般的数学文献中，布尔代数常用格来定义。

一个非空的偏序集〈L，≤〉，如果其中每一对元素x，y都有上确界(记作x∨y或x+y)及下确界(作记x∧y或x·y)，则称〈L，≤〉为格。如果格〈L，≤〉还满足以下两条分配律：

x∧(y∨z)=(x∧y)∨(x∧z)

x∨(y∧z)=(x∨y)∧(x∨z)

则称〈L，≤〉为分配格。格〈L，≤〉中可能有(唯一的)最大元(记作1)和(唯一的)最小元(记作0)。在有0，1(0≠1)的格(L，≤〉中，如果x∧y=0且x∨y=1，则称y为x的补。在分配格中，x若有补，其补必唯一，记作．如果格〈L，≤〉中的每个元素都有补，则称〈L，≤〉为补格。布尔代数就是分配的补格。

布尔代数的形式理论BA一般以∨、∧，－三种运算为基本概念，其语言为=｛0，1，∨，∧，－｝，公理可以有不同的选择，比如下述非逻辑公理是文献中常用的：

I．交换律

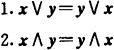
Ⅱ．结合律

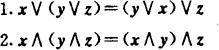
Ⅲ．吸收律

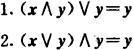
Ⅳ．分配律

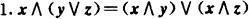
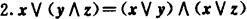
Ⅴ．补律

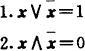
偏序≤不作初始符号，可由∧定义为：

x≤y当且仅当x∧y=x

BA的模型就是布尔代数。1949年A．塔尔斯基证明：BA是可判定的。

以下是逻辑中常用的布尔代数的一些例子：

例1(极小代数) 集合2=｛0，1｝在如下定义的三种运算∨、∧、之下形成一个布尔代数，称为极小代数：

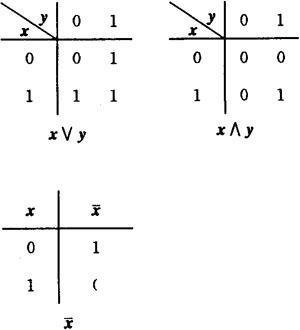
例2(幂集代数) 设X为任意的非空集合，X的幂集P(X)在运算∪、∩、－之下形成一个布尔代数，称为X的幂集代数。幂集代数中的偏序关系就是包含关系。

例3(有穷－补有穷代数) 自然数集ω的全体有穷子集及补集为有穷集的子集，在集合的并、交、补运算之下形成一布尔代数，称为ω上的有穷－补有穷代数(其偏序仍为)。

例4(林登堡代数) 设Φ为全体命题公式的集合，在Φ上定义等价关系≈：对任何α，β∈Φ，

α≈β 当且仅当 ┝aβ．

以［α］表示含有公式α的≈等价类，令

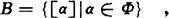
在B上定义运算

以及

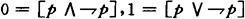
则〈B，0，1，∨，∧，－〉是一布尔代数，其中的偏序是：

［α］≤［β］ 当且仅当 ┝α→β

这个布尔代数称为命题林登堡代数。

理想和滤子是布尔代数中一对极为重要的对偶概念。设B是布尔代数，满足以下三个条件的非空子集FB称为B的滤子：

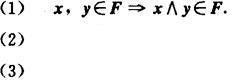
如果滤子F还满足

(4) 对任何x∈B，x∈F或∈F，

则称F为超滤子。

滤子、超滤子的对偶概念为理想和素理想。将上述滤子定义中的∧换成∨，≤换成≥，0换成1，即为理想和素理想的定义。事实上

F是(超)滤子当且仅当I=｛｜x∈F｝是(素)理想。

对于理想和素理想，1932年A．塔尔斯基得到著名的素理想定理：每个理想都可扩充成一个素理想。

素理想定理的(等价的)对偶形式为超滤子定理：

每个滤子都可扩充成一个超滤子。

超滤子定理(素理想定理)是选择公理的一个重要的弱形式。

设B与B’是两个布尔代数，如果存在映射(h：)B→B’使对每个x，y∈B有

h(x ∨ y)=h(x)∨ h(y)

h(x ∧ y)=h(x)∧ h(y)

h(x)=h(x)

则称B与B′同态；如果h是一一对应，则称B与B′同构。

有穷的布尔代数都与某个幂集代数同构，但无穷的布尔代数则未必，例如ω上的有穷－补有穷代数，其基数为，不可能与任何幂集代数同构。关于一般布尔代数与幂集代数的关系，有斯通表示定理。

设X为非空集，X的幂集代数的子代数称为X上的子集域或集合域。对任意的布尔代数B，以SB表示B的全体超滤子所组成的集合。斯通表示定理是说：每个布尔代数B都同构于SB的一个子集域(参见集合代数、布尔值模型、超积、大基数等条)。