哥德尔不完全性定理
关于一阶形式数论(以及更强的形式理论)的不完全性的结果。由K.哥德尔1931年在其著名论文《〈数学原理〉及有关系统中的形式不可判定命题》中给出。
哥德尔的文章针对A.N.怀德海与B.罗素合著的《数学原理》中的形式系统PA证明:
如果PA一致,则存在一个真的一阶数论公式β,使
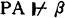
哥德尔的证明可以分成三个部分。
第一部分是哥德尔配数法。哥德尔通过一种能行的方法给每个PA公式α配上一个自然数gn(α),称为α的号码或α的哥德尔数。又用类似的方法给每个有穷的公式序列Φ={φ,…,φ}也配上一个自然数gn(Φ),称为Φ的号码或Φ的哥德尔数。其要点在于,这种配数法是确定的、能行的。也就是说,任给一个公式α(或公式序列Φ),可以具体计算出gn(α)(或gn(Φ));任给一个自然数a,也可以能行地确定a是否是某个公式a(或某个公式序列Φ)的哥德尔数,如果是,则还可进一步写出a(或Φ)(参见哥德尔配数法)。
通过这种配数过程,公式(或公式序列)之间的关系就转化为自然数之间的关系了,于是某些本属于元语言层次的内容就可以在PA内部得到反映。
证明的第二部分是建立“数字可表示”的概念。设 ={0,′,+,·}为PA的形式语言。每个自然数n在PA中都有一个形式表达式(项)
={0,′,+,·}为PA的形式语言。每个自然数n在PA中都有一个形式表达式(项) ,称为n的数字。例如
,称为n的数字。例如 =0,
=0, =0′,
=0′, =0″,
=0″, =
= …,等等。
…,等等。
设A(x,…,x)是一(直观的)数论谓词,如果存在一个PA公式a(v,…,v)使得对每个具体的自然数组(k,…,k)都有
若A(k,…,k)为真,则PA┝α( ,…,
,…, )
)
若A(k,…,k)为假,则PA┝ α(
α( ,…,
,…, ),则称A(x,…,x)为由公式α(v,…v)数字可表示的。
),则称A(x,…,x)为由公式α(v,…v)数字可表示的。
在哥德尔的文章中,大量的篇幅是用来证明若干具体的数论谓词的数字可表示性的。哥德尔事实上给出了原始递归谓词的概念,并证明原始递归谓词都是数字可表示的。现在知道,数字可表示的谓词就是递归谓词。
证明的第三部分就是实际构造一个不可判定命题。哥德尔应用对角线法,构造了一个自指语句G,“G是不可证明的”。这是一个不可判定命题,具体构造过程如下:设γ(v)为恰含一个自由变元的PA公式,其哥德尔数
gn(γ(v))=a
将a的数字 代入γ中的v,得到公式
代入γ中的v,得到公式
γ( ),
),
称为a的自代入。
设A(x,x)是这样一个数论谓词:x是某个恰含一个自由变元的PA公式γ(v)的号码,x是x的自代入γ( )的一个证明(公式序列)的号码(A(x,x)可读作x是x的自代入的证明)。
)的一个证明(公式序列)的号码(A(x,x)可读作x是x的自代入的证明)。
哥德尔证明:
A(x,x)是数字可表示的。
(根据丘奇论题,容易看出A(x,x)是递归谓词。)
也就是说存在PA公式α(v,v)使对任意的自然数a,b
A(a,b)为真,则PA┝α( ,
, )
)
A(a,b)为假,则PA┝ α(
α( ,
, )
)
考虑公式
 vα(v,v)这是一个恰含一个自由变元(v)的公式,设
vα(v,v)这是一个恰含一个自由变元(v)的公式,设
p=gn(
 vα(v,v))
vα(v,v))
则 p的自代入是闭公式β:
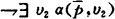
它就是所要的不可判定命题。
首先,β不可证。假如不然,即
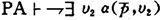
由谓词演算,对任何自然数b都有
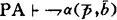
根据A(x,x)的数字可表示性,这意味着对任何自然数b都有
A(p,b)为假,
也就是说p的自代入不可证,
但p的自代入就是β,于是由β可证推得β不可证,矛盾。
其次,β是真的。假如不然,即
 vα(
vα( ,v)为假,由语义定义,这意味着存在一个自然数b使α(
,v)为假,由语义定义,这意味着存在一个自然数b使α( ,
, )为真,如果PA一致,这又意味着
)为真,如果PA一致,这又意味着
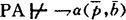
于是根据A(x,x)的数字可表示性,知A(p,b)不会为假,即A(p,b)为真,从而p的自代入β可证,再根据PA的一致性知p的自代入(即β)为真,矛盾。
这就证明了β是一个真公式但不可证。
接着,哥德尔又证明:
假如PA是ω一致的,则
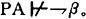
(所谓ω一致是说:对任何公式γ,以下无穷多个公式:
γ( ),γ(
),γ( ),…,
),…,
γ( ),…,
),…, v
v γ(v)不会都是PA定理。)
γ(v)不会都是PA定理。)
后来,J.B.罗塞尔发现ω一致性的假定是不必要的;他另构造了一个闭公式β′,并证明:
如果PA一致,则存在闭公式β′使
PA β′且PA
β′且PA
 β′。
β′。
现在的文献上常按这一方式陈述哥德尔不完全性定理。
哥德尔的文章是逻辑史上最重要的文献之一。它所包含的思想极为丰富,从中派生出来的课题一直延续数十年之久。
哥德尔的证明是针对《数学原理》中的数论系统作出的,但其方法具有普遍意义:任何一个一致的形式理论,只要能够在其中定义递归函数的概念,就一定不完全。这意味着一切比数论系统更强的一阶理论(如公理集合论)都不完全。哥德尔的方法还表明这些不完全的理论都是实质不完全的,也就是说不能靠增加公理的办法把它们补成完全的。无论怎样增加公理,仍能使用哥德尔的方法构造出一个不可判定的命题。
从现代递归论的角度,哥德尔不完全性定理也可按以下方法证明:以TH表示PA的(闭)定理集,以TR表示数论标准模型的真句子集。如果PA一致,则
TH TR。
TR。
在递归论中可以证明TH是递归可枚举集,而TR是产生集(因而不是递归可枚举集),从而
TH≠TR
哥德尔的论文中还提出了一个更强的结果,通常称为第二不完全性定理:
如果PA一致,则这种一致性不能在PA内证明。(这一结果当然也适用于比PA更强的形式理论,如ZF。)
一般认为哥德尔的这一结果宣告希尔伯特计划是行不通的(参见希尔伯特计划和形式主义两条)。
哥德尔当时并没有给出第二不完全性定理的形式证明,只是非形式地勾勒出一个证明的轮廓。由于哥德尔的结果很快获得广泛的接受,所以他本人始终没有给出第二定理的形式证明。以后D.希尔伯特和P.贝尔奈斯(1939年),S.费弗尔曼(1960年)都曾给出第二不完全性定理的证明,均长达四十余页。