哥德尔-贝奈斯公理系统
一个处理直谓类的集合论公理系统。这个系统首次由V.诺依曼在1925年提出,后经P.贝奈斯在1937年开始发表的一组论文中修改补充,而在K.哥德尔1940年的专著中系统地塑述,文献中通常称为诺依曼-贝奈斯-哥德尔系统,记作NBG;也常称为哥德尔-贝奈斯系统,记做GB。与ZF(参看策尔梅洛-弗兰克尔公理系统)不同,GB是一个有穷的集合论公理系统。GB系统的初始概念为类和集合,分别用Cla和 表示,二元关系∈,以及两类变元——类变元,用大写的字母X,Y,Z,……表示,集合变元,用小写的字母x,y,z,……表示,及逻辑符号(联接词、量词和等词=)。GB的语言是一种二种类的集合论语言。集合也是类,是可以作为其它类的元素的类。不是集合的类、即不能作别的类的元素的类,称为真类。GB系统的原子公式为:x=y,x=Y,X=y,X=Y,x∈y,x∈Y,X∈y,X∈Y,Cla(X),
表示,二元关系∈,以及两类变元——类变元,用大写的字母X,Y,Z,……表示,集合变元,用小写的字母x,y,z,……表示,及逻辑符号(联接词、量词和等词=)。GB的语言是一种二种类的集合论语言。集合也是类,是可以作为其它类的元素的类。不是集合的类、即不能作别的类的元素的类,称为真类。GB系统的原子公式为:x=y,x=Y,X=y,X=Y,x∈y,x∈Y,X∈y,X∈Y,Cla(X), (X)。〈x,y〉,〈x,y,z〉分别表示有序对、有序三元组(参看关系)。GB的公理分为五组。
(X)。〈x,y〉,〈x,y,z〉分别表示有序对、有序三元组(参看关系)。GB的公理分为五组。
A组公理
(1)Cla(x) (它是说每一集合都是类);
(2)X∈Y→ (X) (若X是类Y的元素,则X是一集合,即类的元素都是集合);
(X) (若X是类Y的元素,则X是一集合,即类的元素都是集合);
(3) x(x∈X
x(x∈X x∈Y)→X=Y(类是由它的元素决定的。这是类的外延公理);
x∈Y)→X=Y(类是由它的元素决定的。这是类的外延公理);
(4)无序对公理 对任意集合x,y,都存在一集合z,z的元素恰好是x和y。
B组公理(类的存在公理)
(1) X
X x
x y(〈x,y〉∈X
y(〈x,y〉∈X x∈y)((1)是关于∈关系的公理;它肯定存在一个类,其元素为第一元与第二元有关系∈的有序对。)
x∈y)((1)是关于∈关系的公理;它肯定存在一个类,其元素为第一元与第二元有关系∈的有序对。)
(2)类的交公理 对任意的类X,Y,都存在一类Z,Z是X与Y的交。即: X
X Y
Y Z
Z u(u∈Z
u(u∈Z u∈X∧u∈Y);
u∈X∧u∈Y);
(3)类的补公理:对于任意的类X,X的补也是一类,换言之,X的补类存在。即: X
X Y
Y u(u∈Y
u(u∈Y u
u X)(注意,一集合的补就不是集合了);
X)(注意,一集合的补就不是集合了);
(4)Dom公理 对于任一X,它的元素有序对的第一元组成一类,即{x| y(〈x,y〉∈X)}是一类。(这个类为DomX)
y(〈x,y〉∈X)}是一类。(这个类为DomX)
(5)直积公理  X
X Y
Y x
x y(〈y,x〉∈Y
y(〈y,x〉∈Y x∈X);
x∈X);
(6)逆公理 对任一类X,它的逆X也是一类,即: X
X Y
Y x
x y(〈x,y〉∈Y
y(〈x,y〉∈Y 〈y,x〉∈X);
〈y,x〉∈X);
(7)对任一类X,存在一类Y,对任意的集合x,y,z,有〈x,y,z〉∈Y,当且仅当〈y,z,x〉∈X,即, X
X Y
Y x
x y
y z(〈x,y,z〉∈Y
z(〈x,y,z〉∈Y 〈y,z,x〉∈X);
〈y,z,x〉∈X);
(8)对任一类X,存在一类Y,对任意的集合x,y,z,有〈x,y,z〉∈Y,当且仅当〈x,z,y〉∈X,即: X
X Y
Y x
x y
y z(〈x,y,z〉∈Y
z(〈x,y,z〉∈Y 〈x,z,y〉∈X)。
〈x,z,y〉∈X)。
C组公理(集合存在公理)
(1)无穷公理 存在一无穷集合。即: x(x≠Φ∧
x(x≠Φ∧ y(y∈x→
y(y∈x→ z(z∈x∧y
z(z∈x∧y z)))(空集Φ和关系
z)))(空集Φ和关系 都是系统中可定义的);
都是系统中可定义的);
(2)并集合公理 任一集合的元素的元素组成一集合,即: x
x y
y u
u v(u∈v∧v∈x→u∈y);
v(u∈v∧v∈x→u∈y);
(3)幂集合公理 任一集合的所有子集合组成一集合,即: x
x y
y u(u
u(u x→u∈y);
x→u∈y);
(4)替换公理 对于描述一一对应的类X(即对任意的x,至多有一y使得〈x,y〉∈X),若把X的元(有序对)的第一元限制在一给定的集合S中,即令DomX=S,则X的元的第二元也组成一集合S。
不难看出,上述公理(1)~(3)分别与ZF中相应的公理相同。公理(4)与ZF中的替换公理模式相似,不同的是在ZF的公理模式中的前提是一具有一对一性质的公式,公式有无穷多个,因此是无穷多条公理构成的一个模式;而这里的公理(4),作前提的是具有一对一性质的类,(4)是一条公理,不是模式。GB中所以能用一个公理取代一个公理模式,是由于有B组公理。不难验证,B组公理是对应于公式的通常运算的一组公理。
D组公理
基础公理 对任一不空的类X,都有一集合y∈X使得y与X不相交。(基础公理与ZF中的正则公理相似,不同点在于这里是类的正则公理。)
E组公理
选择公理 存在一个具有一对一性质的类X,对所有集合x,若x不空,则存在一y使得y∈x并且〈y,x〉∈X。
这是一个比通常的选择公理更强的选择公理,因为它提供了用一个关系,就从所考虑的论域的每一集合中同时选择一个元素。用这个公理,能够证明,集合的全域是可以良序的。它称为整体选择公理,而通常的选择公理也称为局部选择公理。
这5组公理中,没有公理模式,因此是一有穷的公理系统。这是GB系统重大特点之一。它规定真类(如所有序数组成的类,所有基数组成的类)不能作为类的元素,从而摆脱了以往的悖论。已经证明,GB与ZF是等协调的,它是ZF的一保守扩充。
令φ(x)为上述二种类集合论语言的一个公式,x在其中自由出现,X不在其中自由出现,并且φ(x)中不含有类量词。公式
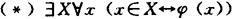
称为直谓类的概括公理模式。把GB中的B组公理换成公理模式(*),所得的结果系统记为GB。GB是一个无穷的公理系统。不难证明,这两个系统是等价的,也就是说,对二种类集合论语言中的任一语句A,都有:GB┝A当且仅当GB┝A。把GB中的直谓类的概括公理模式(*)换成非直谓类的概括公理模式(也可以说是把(*)加强为非直谓类的公理模式)所得的结果系统为QM(奎因-莫尔斯公理系统)。已经在QM中证明了GB系统的协调性。