基数
又称势,集合论基本概念之一,是日常语言中用以表示多少的数这一概念的推广和发展。按照G.康托尔的原意,集合A的基数是一切与A具有等势关系的集合(即存在一个双射,这一集合A的全部元素映到另一集合的全部元素)的共同特征,是对A的元素进行属性及次序双重抽象之后的结果,所以用 表示(也常用|A|表示)。G.弗雷格与B.A.W罗素分别在1884年与1902年把A定义为所有与集合A等势的集合所成的类,即
表示(也常用|A|表示)。G.弗雷格与B.A.W罗素分别在1884年与1902年把A定义为所有与集合A等势的集合所成的类,即 ={B|B~A},这是一真类。这一定义虽然形式简单明了,但它不是一集合,不能是ZF系统中的对象。1928年J.冯·诺伊曼建议用一个特殊的与A等势的集合,即所有与A等势的序数中最小的那个作为A的基数,这样的序数称为初始序数。根据选择公理,对于任何集合A,它所对应的初始序数是必定存在并且是唯一的。由此,基数就是特殊的序数了。两个集合A、B具有相同基数的充要条件是A~B,这完全符合康托尔的原意。当一集合的基数为有穷序数时,称该基数为有穷基数,即自然数,否则称为超穷基数或无穷基数。它们所对应的集合分别称为有穷集合与无穷集合,在选择公理之下,可以证明集合A为无穷的充要条件是存在A的一个真子集合A,使得A~A。与自然数集合等势的集合称为可数集合,它的基数为ω,习惯上常用
={B|B~A},这是一真类。这一定义虽然形式简单明了,但它不是一集合,不能是ZF系统中的对象。1928年J.冯·诺伊曼建议用一个特殊的与A等势的集合,即所有与A等势的序数中最小的那个作为A的基数,这样的序数称为初始序数。根据选择公理,对于任何集合A,它所对应的初始序数是必定存在并且是唯一的。由此,基数就是特殊的序数了。两个集合A、B具有相同基数的充要条件是A~B,这完全符合康托尔的原意。当一集合的基数为有穷序数时,称该基数为有穷基数,即自然数,否则称为超穷基数或无穷基数。它们所对应的集合分别称为有穷集合与无穷集合,在选择公理之下,可以证明集合A为无穷的充要条件是存在A的一个真子集合A,使得A~A。与自然数集合等势的集合称为可数集合,它的基数为ω,习惯上常用 表示。整数集合Z,有理数集合Q,整系数多项式集合A〔x〕,代数数集合,n维欧氏空间E中的格子点集合等都是可数集的例子。每一个无穷集合都存在可数子集合,而可数集合的任一无穷子集合必为可数集合。在基数序的意义下,
表示。整数集合Z,有理数集合Q,整系数多项式集合A〔x〕,代数数集合,n维欧氏空间E中的格子点集合等都是可数集的例子。每一个无穷集合都存在可数子集合,而可数集合的任一无穷子集合必为可数集合。在基数序的意义下, 是最小的无穷基数,即可数集合是最小的无穷集合。可数集合与有穷集合一起合称至多可数集合,非可数的无穷集合称不可数集合。无理数集合,超越数集合,区间(a,b)中的点集合,〔0,1〕上的连续函数集合C〔0,1〕,n维空间E的点集合,定义在〔a,b〕上的函数集合等等都是不可数集合的例子。所有可数序数所组成的集合也是一不可数集合。
是最小的无穷基数,即可数集合是最小的无穷集合。可数集合与有穷集合一起合称至多可数集合,非可数的无穷集合称不可数集合。无理数集合,超越数集合,区间(a,b)中的点集合,〔0,1〕上的连续函数集合C〔0,1〕,n维空间E的点集合,定义在〔a,b〕上的函数集合等等都是不可数集合的例子。所有可数序数所组成的集合也是一不可数集合。
基数的初等运算及性质 设α,β为两个基数,A,B为两个集合,|A|= α,|B|=β,可以定义基数的大小关系及和、积、幂等运算如下:
α≤β当且仅当存在一个从A到B的单射函数;
α<β当且仅当α≤β且α≠β;
α+β=|{0}×A∪{1}×B|
其中二集合C,D的叉乘为:C×D={<x,y>|x∈C∧y∈D};
α·β=|A×B|;
α=|A|,
其中A={f|f:B→A}。
在上述定义中,虽然形式上需要通过集合A,B来表述,但事实上它们都只与α,β有关,而不依赖于A,B的选取。即对于任何集合A,B,只要|A|=α,|B|=β,所得的结果就保持不变。这就保证了定义的合理性。此外,和与积还能推广到任意基数列α(β<γ)。设β<γ时|A|=α则可定义

对于任何基数α,β,γ,下列性质成立。
①传递性:若α≤β且β≤γ则α≤γ。
②自反性:α≤α。
③反对称性:若α≤β且β≤α则α=β。
④强连结性:α≤β与β≤α二者必居其一。
⑤结合律:α+(β+γ)=(α+β)+γ。
α·(β·γ)=(α·β)·γ。
⑥交换律:α+β=β+α;α·β=β·α。
⑦存在恒等元:0+α=α;1·α=α。
⑧分配律:α(β+γ)=α·β+α·γ。
⑨同底幂的积:α·α=α。
⑩幂的幂:(α)=α。
⑾积的幂:(α·β)=α·β。
性质①~④说明基数的≤是一个全序关系,其中性质③称为康托尔-伯恩斯坦定理,它是集合论中的一个重要定理,可用以确定若干集合的基数。1895年康托尔给出了这一命题的等价形式:设A,B为两个集合,若A与B的子集合B等势,B与A的子集合A等势,则A与B等势;并在基数可比较的前提下给予证明。1896年F.W.K.E.施罗德在一篇论文的摘要中提到这条定理。他于1898年发表的证明虽不借助于基数的可比较性,但仍不完善。第一个满意证明是伯恩斯坦在1898年给出的,所以有些数学家称它为施罗德-伯恩斯坦定理。性质④称为基数比较定理,它是选择公理的等价命题之一,最初由G.康托尔提出:设A、B为两个集合,则或者A与B的某一子集合B等势或者B与A的某一子集合A等势,两者必有一个成立;并用以证明性质③。1915年由F.M.哈尔托格斯给予证明。关于基数的序与运算的其他重要性质还有:⑿对于任何基数κ,总存在一个比κ大的基数λ,即不存在最大的基数。这一性质是1873年首先由康托尔以下述形式提出的:任何集合A的幂集合P(A)具有比A大的势,即|A|<|P(A)|,故称康托尔定理。由于在集合P(A)与集合2间存在自然的双射函数,所以这个性质也可表为2>κ,其中x=|A|。于是,康托尔把无穷分成无穷多个严格递增的等级,奠定实无穷在数学研究中的地位。他在证明中所使用的对角线方法,也具有重要的方法论意义。已经知道最小的无穷基数是 ,并用
,并用 表示大于
表示大于 的最小基数,用
的最小基数,用 表示大于
表示大于 的最小基数。一般地,设α是任一序数,并且对于任何小于α的序数β,
的最小基数。一般地,设α是任一序数,并且对于任何小于α的序数β, 均已定义,则当α为某一β的后继序数时,规定
均已定义,则当α为某一β的后继序数时,规定 是大于
是大于 的最小基数,称为后继基数;当α为极限序数时,规定
的最小基数,称为后继基数;当α为极限序数时,规定 ,称为极限基数。(参见阿列夫)这样就建立起序数与无穷基数之间的一一对应关系。⒀基数的加、乘运算具有许多通常熟悉的性质,如结合律,交换律,分配律等,但有些重要性质,例如单调律,却仅对有穷基数,即自然数成立。设λ,κ为任意基数,λ≥κ≥1,λ≥
,称为极限基数。(参见阿列夫)这样就建立起序数与无穷基数之间的一一对应关系。⒀基数的加、乘运算具有许多通常熟悉的性质,如结合律,交换律,分配律等,但有些重要性质,例如单调律,却仅对有穷基数,即自然数成立。设λ,κ为任意基数,λ≥κ≥1,λ≥ ,则λ·κ=λ+κ=λ。这一结果与下述命题等价:对于任何无穷基数κ,κ·κ=κ+κ=κ,即任意κ个基数为κ的集合的和集,其基数为κ;或者,任意不超过κ个、基数不超过κ的集合的和集,其基数不超过x。特别地,当κ=
,则λ·κ=λ+κ=λ。这一结果与下述命题等价:对于任何无穷基数κ,κ·κ=κ+κ=κ,即任意κ个基数为κ的集合的和集,其基数为κ;或者,任意不超过κ个、基数不超过κ的集合的和集,其基数不超过x。特别地,当κ= 时,就有任意可数个可数集合的和集是可数集;或至多可数个至多可数集合的和集是至多可数的。上述命题是选择公理的一个推论。将它深化一步,可得:对于任何序数α,
时,就有任意可数个可数集合的和集是可数集;或至多可数个至多可数集合的和集是至多可数的。上述命题是选择公理的一个推论。将它深化一步,可得:对于任何序数α, 与
与 成立。⒁把基数的运算与序相结合而得到的结果,最重要一条是寇尼希引理(参见寇尼希引理)。
成立。⒁把基数的运算与序相结合而得到的结果,最重要一条是寇尼希引理(参见寇尼希引理)。
正则基数与奇异基数 一无穷基数κ,当κ的共尾性特征数cf(κ)(参见序数)等于κ时,就称κ为正则基数,当cf(κ)<κ时,就称κ为奇异基数。
弱不可达基数 一正则基数κ,当所有小于κ的无穷基数按从小到大的次序排列所得的序型为一极限序数时,就称κ为弱不可达基数。
强不可达基数 一无穷基数κ,如果满足下述三个性质:
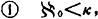
②若λ<κ,则2<κ,
③若S为一基数集合, <κ,
<κ, λ∈Sλ<κ,则|∪S|<κ,
λ∈Sλ<κ,则|∪S|<κ,
那么就称κ为一强不可达基数,也称它为一不可达基数。
与基数有关的命题中有许多重大的结果和重要命题。(参见连续统假设、选择公理和强无穷公理)。